I wanted my simulation pages to have accurate positions of the planets in the solar system. I found that there were two approaches to this:
Johannes Kepler formulated his laws of planetary motion in the early 17th Century. These stated that planets would follow an elliptical orbit with the sun at one of the ellipses foci. The position of the planet at a time is given by an equation involving six parameters (the orbital elements). I found a number of online resources, including Schlyter, P. (2020) that explained the calculations. For the calculations, the equations generally use the number of Julian days (1 solar day = 24 hours) from the latest "J2000 astronomical epoch" (1 January 2000, 12:00:00 UTC). It is relatively easy to convert Julian dates into standard calendar dates.
For coordinate systems, it is traditional to use the ecliptic coordinate system when looking at the whole solar system, but an equatorial coordinate system when looking at just the earth and moon.
The position of the planets have been traditionally expressed in Astronomical Units (“au”) where 1 au is equal to the average distance between the Earth and the Sun. For convenience, I converted these to km, using the standard International Astronomical Union value of 1 au = 149587870.7 km.
I wanted to use accurate physics to predict the motion of a spacecraft travelling around the solar system, so that it could illustrate different orbits and orbital manoeuvres. For practical purposes, using Newton's laws of motion and universal gravitation is adequate without the complexity of Einstein's theory of General Relativity (Braeunig, Orbital Mechanics 2017).
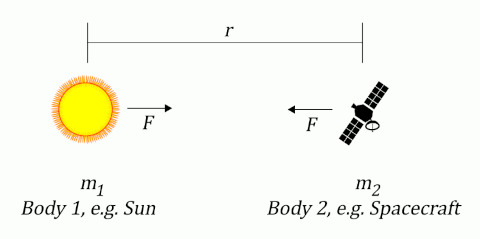
Any two bodies with mass m1 and m2, separated by a distance r, are subject to a mutually attractive force of gravity given by:
Where G is the gravitational constant and is equal to approximately 6.674 x 10-11 m3kg-1s-2. When one of the bodies has a significantly larger mass than the other (e.g. when one is a planet or the Sun), then the force has virtually no effect on the massive body and the acceleration of the smaller body is given by:
This equation gives the acceleration of the small body in m/s2. The acceleration will be directed towards the large body. The term in the numerator of this equation is commonly referred to as "GM" and the values of GM for the Sun and each planet can be calculated from the estimated mass of the body. It is also available directly from a number of authoritative sources (NASA Goddard Space Flight Center, 2021) scaled to produce acceleration in km/s2.
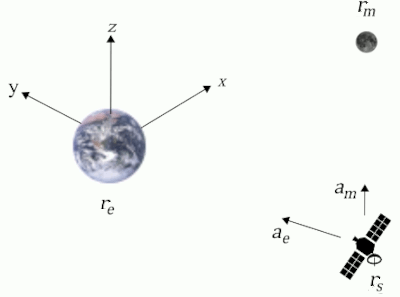
In the simulator, the spacecraft will be subjected to gravitational attraction from all of the planets in the solar system (although the distant planets will have little influence). To simplify calculations, I used vectors as shown in the diagram below.
The net acceleration acting on the spacecraft can be obtained by taking the vector sum of the acceleration from each massive body - the Sun and planets in the Solar System - (Gould H. et al 2017), i.e.
Where a is the acceleration of the spaceship GMb is the mass of the planet multiplied by the universal gravitation constant, ps is the vector position of the spaceship and pb is the vector position of each planet.
The table below shows the main technologies and tools that I used when creating my web page.
